光技術情報誌「ライトエッジ」No.39(2013年6月発行)
光技術コンタクト(日本オプトメカトロニクス協会)
(2012年10月)
光線逆方向追跡と3つの式
後藤 学
標題は、照度(明るさ)の計算に関することです。
通常、照度計算の際は、光源から照度を知りたい点(観測点)へ向けての光線を考えますが、観測点から光源に向けて、光線を逆方向に追跡して照度を考えると言うことです。例えば、レンズを使って照度を上げる場合、集光するから照度が上がると考えるのではなく、観測点から光源を見ると、光源が大きく見えるから照度が上がると考えることです。勿論、集光すると考えることを第一にするのですが、大きく見えると考えると非常に便利なことがあるので、“光線逆方向追跡のすすめ”と言うつもりで本稿を書いてみました。
1970年に、ガウス分布状の輝度(まぶしさの度合い)を持った棒状の光源と、円柱状の反射面を使用したサーチライトで、そのランプの位置と照度分布の関係を計算したことがあります。光源から光線を追跡すると、どうしても観測点以外に到達する光線まで追跡をしてしまいます。照度計算は膨大な計算が必要ですし、当時、職場には関数計算が出来ない電卓しか無かったので、無駄な計算は出来ません。また、余計な所の計算をしなければならないのは、どこかが本質的に間違っているのではないか、観測点から見て、その四方八方の環境が決まれば照度も決まる筈、と思いました。そこで観測点から光線を逆方向に追跡して、照度を計算する方法を模索し、辿り着いたのが、「照度は観測点から四方八方を見て、その方向に見える微小光源の輝度に微小立体角を掛けたものを足し合わせれば良い」と言うことと、「輝度は光学系(反射屈折の法則)では不変」の2点でした。
これを使って、観測点から見たサーチライトの円柱状反射面を微小立体角で分割し、光線を逆方向に追跡し、光源にぶつかった所の輝度に反射率を掛けて足し合わせ、照度を計算しました。幸い、照度分布は測定結果と良く合い、ランプと円柱状の反射面の相対位置を変えると、照度分布がどう変わるかが良く分かったと記憶しています。
ここからが3つの式になりますが、上記のことを、極座標(r,θ,¢)で表現すると、照度はE=∫∫Bcosθsinθdθd¢になります(図1)。これが第一の式です。
Bは観測点から見た(θ,¢)方向の輝度であり、cosθは観測面の傾き補正、sinθdθd¢は微小立体角です。これが光線逆方向追跡の考え方の照度の基本式です。
この式は、式の中に r即ち光源までの距離が無いことが特徴的です。コンピューターで照度計算する際に、この式が非常に便利なのは、式が単純明快なのと、照度計算する必要のない場所への光線追跡が完全に除外され、計算量が少ないことです。照度の定義は単位面積を単位時間に通過する光量ですが、私はこの式を定義の次に重要な式であると考えています。その後、照明計算ソフトが市販されるようになりましたが、光線逆方向追跡では無く、光源から大量の光線を飛ばし、観測点の一定の面積にいくつ光線が入るかで照度計算をするものでした。
次に、円盤光源が観測点より半角θで見える位置にあり、輝度が等方一様で B である場合、照度はE =∫∫Bcosθsinθdθd¢=πBsin2θになり、E=πBsin2θとなります(図2)。これが第二の式です。
輝度は不変ですから、この式から、輝度Bの光源を使用した光学系での最大照度E=πBが分かります。お客様から、「光学系で照度を上げて欲しい」と言う話があった時に、その場で「ご要求の照度は無理です」と答えると、「努力もせずに無理と言うな」と強くお叱りを頂くことがあります。その場合、E=πBsin2θより、限界の照度が分かることを説明すると共に、「太陽光をレンズで集光すると紙が燃える位高い照度が得られるが、蛍光灯では紙は燃えないでしょう」と付け加えることにしています。なんとなく納得して頂き、怒りが半減するようです。繰り返しになりますが、円盤光源に観測点を近づけ、円盤光源の表面に達すると、θ=90度になり、E =πBとなります。輝度は光学系では透過率、反射率で落ちることはあっても、高くはならないですから、これが輝度Bの光源の限界の照度になります。光出力が十分であっても、サイズと光を発散する角度が大きい光源は輝度が小さく、高い照度は得られません。また、この式から、光源が近くなると照度は高くなり、遠くなると低くなるのは、光源の見込み角度が大きくなったり、小さくなったりするからと言えます。凸レンズや凹レンズで集光したり発散させたりして照度が変るのも、光源の見込み角が大きくなったり小さくなったりしているからです。
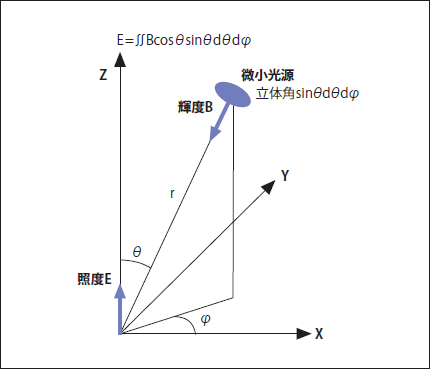
図1. 原点に於けるXY平面の照度
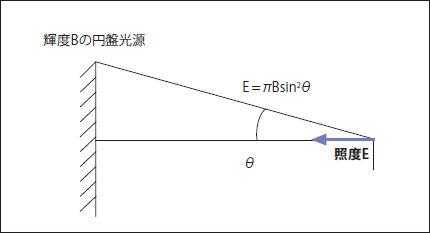
図2. 円盤光源の照度
この式を使って、太陽の表面放射照度を計算して見ます。
地球大気圏外で、太 陽の方向を向いた面での放射照度は約1.4kw/m2であり、太陽の半径の見込み角は約0.25度です。これだけで、E=πBsin2θより、太陽表面の放射照度は約73500kw/m2と計算されます。また、半径の見込み角30度の凸レンズで太陽光を集光した時の照度は、18400kw/m2になります。
この様に、この式が便利なのは、測定の難しい太陽までの距離や半径が分からなくても、簡単に測定出来る見込み角が分かれば、照度が計算できる所にあります。照度は点光源からの距離の自乗に反比例する(距離の自乗則)と言う照度計算の有名な法則があります。この距離の自乗則は光量保存(エネルギー保存)から来る最も基本的な式ですが、光源に大きさがある場合は、E =πBsin2θに於いてθが小さい(光源が小さい)場合の近似であると考えることが出来ます。
更に、この式と光量保存から、D×NA=一定が導かれます(面積×照度は一定、これの平方根)。これが第三の式です(図3)。
Dは光源や観測面の光芒の直径、NA=sinθ、θは集光角、発散角あるいは見込み角です。我々はこれを、「DNA(遺伝子)は保存する」と洒落て、悦に入っています。エタンデューと言う概念を知らずに、これを使っていましたが、これを自乗すると、一般に言われている「エタンデュー(光芒面積×光源の立体角)は保存する」と同じになります(立体角が小さい時)。
投影レンズの倍率とNAの関係はこの式そのものですが、この式は、結像関係が無い場合にも成立します。図3で言えばDNA=D′N′A′です。図3のような集光鏡を使用した光学系では、例えば、投影レンズの像側NA=0.1、像の直径100mmであれば、途中の光学系はどうあれ、DNA=D″N″A″であり、集光鏡に同じような考え方を適用すれば、光源の光を有効に利用するには、光源のサイズは5mm程度である必要があることが分かります。それ以上の大きさの光源の光は利用出来ません。光源の光出力がいかに大きくても、そのサイズが大きいと、光を有効に利用出来ず、像面の照度を上げることが出来ない、という結果になります。
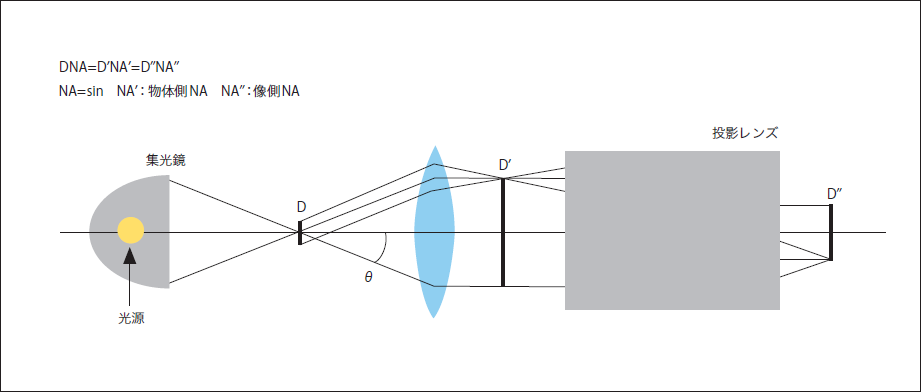
図3. DNAは保存する
以上、光線を逆方向に追跡して考えることで、便利なことがあることを述べてきました。
迷路のクイズは、当然の如く、スタートからのみならず、ゴールからも解を探ると思います。これと同じように、光線を逆方向に追跡する考え方も有用であると言えます。更に、照度計算においては、スタートから解を探すと非常に厄介な問題でも、ゴールから解を探すと、殆ど迷う事無く、一本道に思えるように、解が得られる場合が間々あります。光線逆方向追跡を勧める所以です。
3つの式に代表される、光線逆方向追跡の考え方に非常にお世話になったことに感謝しつつ、逆方向から考えることをお勧めしたいと思います。
論文を探す
今号では、各種の光源(半導体露光用EUV、複写機用LED、高輝度・長寿命・高安定のLDLS、光加熱用ハロゲンヒータなど)や、光の装置・システム(インターポーザ基板用露光装置、スマートフォン・タブレット端末用UVキュア、新規蛍光免疫素子Q-bodyによる薬物検出システムなど)など、2012年春から2013年春にかけて発表した技術や市場動向の論文15件を掲載しました。
シリーズ「大学研究室を訪ねて」では、新しい機能性タンパク質と有機メソッドの創製に挑む、東京工業大学資源化学研究所の上田先生をお訪ねし、開発に成功され、今、話題を集めているQ-bodyを用いた免疫測定法をご紹介しております。
(2013年06月)


